One of the biggest shortcomings of chess engines is that they cannot evaluate how sharp or difficult to play a position is. If there is only one narrow and hard to find path to equality, the engines will still evaluate the position as a draw just like an easy theoretical draw. However, as humans we see these situations very differently. So I tried to evaluate how sharp (or complicated) a position is using Leela’s WDL.
What is WDL?
The chess engine Leela Chess Zero evaluates positions not based on a centipawn score but on the probability to win, draw or lose. This information is presented as WDL which are three numbers that represent the probability of winning, drawing and losing (these numbers are between 0 and 1000 and add up to 1000).
When these numbers are represented as a single evaluation value, some information gets obscured: a game with a (nearly) 100% draw probability gets evaluated as equal but also a game with a 50% win and a 50% loss percentage. My idea was to come up with a formula that looks at the relation between the WDL values and gives a sharpness score based on them.
How I got a sharpness score
I converted the WDL values to a single sharpness score with the following formula:
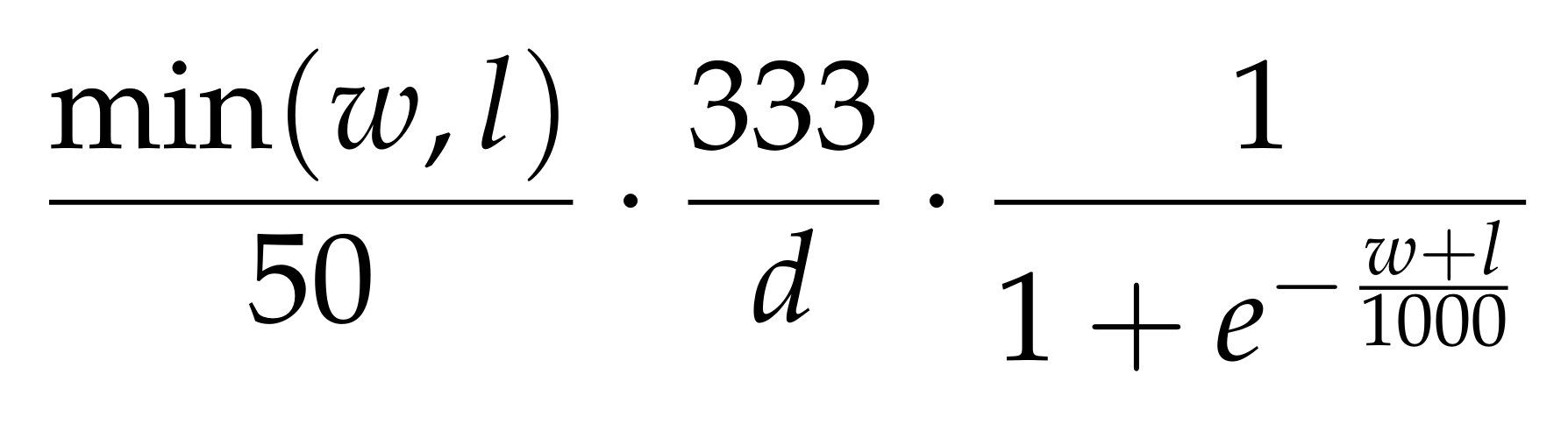
The basic idea is to get a function with the shape of a sigmoid function. The additional factors are there to scale the function:
- A higher minimum of the win/loss will increase the sharpness: if only one side has winning chances, the position isn’t too complicated
- A higher draw percentage leads to a lower sharpness values
Note that all these values and even the whole function are probably not optimal but it’s the best that I could come up with.
An Example
This position is from the game Caruana-Vachier-Lagrave, 2021:
White to play
White is a piece and three pawns down but the position is very dangerous for black. Stockfish gives an evaluation somewhere between -0.5 and -1 at around depth 40 but looking at the position makes it clear that the character of the game is very different from a slight positional advantage for black.
Leela gives WDL values of [333, 227, 440] (at 5000 nodes) which leads to a sharpness value of 6.65. This means that it evaluates the position as being very complicated. Together with the classical evaluation, this gives a fuller picture of the actual situation: black has a slight advantage but the position is very complicated so the objective evaluation is less relevant.
I will look at further examples in a future blog post. Now I want to look at the limitations of this method.
Limitations
One part that I ignored until now is that Leela has to evaluate the position with a certain number of nodes. But what is the best number of nodes? More nodes to get a more accurate representation or fewer nodes that the evaluation is closer the the level of humans?
In the following table you can see the WDL and sharpness score for a variety of numbers of nodes (note that the WDL is from white's perspective):
| Nodes | WDL | Sharpness |
|---|---|---|
| 1000 | [181, 146, 673] | 5.75 |
| 3000 | [319, 213, 468] | 6.82 |
| 5000 | [333, 227, 440] | 6.65 |
| 10000 | [279, 206, 515] | 6.18 |
| 20000 | [255, 207, 538] | 5.62 |
| 50000 | [223, 274, 503] | 3.64 |
| 100000 | [215, 277, 508] | 3.46 |
The table shows how Leela’s thinking - and with it the sharpness - changes over time: first it thinks that white is pretty much lost, but with 3000 nodes it realises that it’s not so clear and as a consequence the sharpness increases. But after 5000 nodes the win percentage starts to decrease and with it the sharpness. At 50000 nodes the draw percentage makes a huge jump up and the sharpness sinks further.
This makes the question regarding the number of nodes more complicated since it's not clear which value is the best. I think that the sweet spot is
somewhere in the the range of 3000-5000 nodes.
If you have any questions or suggestions, feel free to contact me on twitter.